Selected simulations performed with the Spectral Einstein Code
The following table lists some binary-black-hole (BBH) cases that we have evolved with the SXS collaboration's Spectral Einstein Code (SpEC), grouped into non-spinning, non-precessing and generic configurations. For the initial spin parameters S1/M12 and S2/M22, the z direction is parallel to the orbital angular momentum. In the "Merger" column, "Yes" means the simulation has evolved until the merged hole settles into its final state; otherwise the simulation has stopped about one orbit before merger. Click on the numbers in the "References" column to view the corresponding arXiv eprints.
| Case | M2/M1 | S1/M12 | S2/M22 | Norbits | Merger? | References | Comments |
|---|---|---|---|---|---|---|---|
| N1 | 1 | 0 | 0 | 16 | Yes | 1, 2, 3, 4, 5 | a |
| N2 | 2 | 0 | 0 | 15 | Yes | 4, 5 | a, b |
| N3 | 3 | 0 | 0 | 15 | - | 4, 5 | a, b |
| N4 | 4 | 0 | 0 | 15 | - | 5 | a |
| N5 | 6 | 0 | 0 | 8 | Yes | 5 | a |
| N6 | 1 | 0 | 0 | 17 | - | ||
| S1 | 1 | 0 | 0.5ez | 15 | - | c | |
| S2 | 3 | 0 | 0.5ez | 14 | - | c | |
| S3 | 1 | -0.4ez | -0.4ez | 11 | Yes | 5, 6 | a |
| S4 | 1 | 0.4ez | 0.4ez | 15 | Yes | 5 | a |
| S5 | 1 | 0.1ez | 0.1ez | 18 | - | ||
| S6 | 1 | 0.2ez | 0.2ez | 19 | - | ||
| S7 | 1 | 0.3ez | 0.3ez | 19 | - | ||
| S8 | 1 | 0.5ez | 0 | 15 | - | ||
| G1 | 1 | -0.5ex | -0.5ez | 6.5 | - | precessing | |
| G2 | 2 | 0.2(ez-ex)/√2 | -0.4(ez+ey)/√2 | 8.5 | Yes | 5, See below | generic |
| G3 | 5 | 0.24ex-0.19ey-0.148ez | 0 | 6 | - | generic, d | |
| G4 | 2.9622 | 0.24ex-0.19ey-0.148ez | -0.158ex+0.370ey-0.045ez | 6.25 | - | generic, d | |
| G5 | 2 | -0.349ex-0.446ey+0.565ez | 0 | 3 | - | generic, |S1/M12|=0.8, d |
Comments
- We and collaborators are currently using this simulation’s numerical-relativity waveform to underpin the effective-one-body parametrized analytical fit (Buonanno et. al.) and also the phenomenological parametrized analytical fit (Chen, Hannam, Husa, Parmeswaran) for future LIGO data analysis.
- An earlier 8-orbit version of this run has been used for calibrating EOB waveforms to numerical-relativity waveforms in Buonanno et al [Phys. Rev. D 79, 124028 (2009), arXiv:0902.0790].
- These ongoing runs are expected to proceed through about 15 orbits before merger.
- These simulations are being used as test cases for automating the process of generating initial data, interpolating onto the evolution grid, and evolving through inspiral, merger, and ringdown.
Selected figures for Case G2
| M2/M1 | S1/M12 | S2/M22 | Norbits |
|---|---|---|---|
| 2 | 0.2 (ez - ex)/√2 | -0.4 (ez + ey)/√2 | 8.25 |
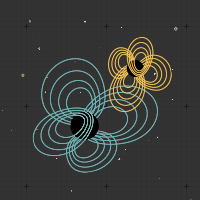
The following plots illustrate some of the features of case G2, which is an evolution of generic binary-black-hole initial data. The initial masses and spins for this simulation are summarized in the above table. The total number of orbits for this simulation is also shown.
Horizon trajectories during inspiral
The trajectories of hole 1 (blue) and hole 2 (red). Specifically, the centers of the apparent horizons in the asymptotically inertial coordinates of the simulation. The z=0 plane is shaded translucent gray; portions of the trajectories below z=0 then appear darker than portions of the curves that are above z=0.
Spin precession during inspiral
The evolution of the spin directions for hole 1 (blue) and hole 2 (red). The tips of unit vectors (in the asymptotically inertial coordinates used in the simulation) trace out paths on the unit sphere (translucent gray).
Horizon masses and spins during inspiral
The mass ratio and dimensionless spins are nearly constant throughout the 8.25 orbits of the inspiral shown here (with the merger occurring shortly thereafter). The axes are normalized by the total Arnowitt–Deser–Misner (ADM) mass of the system.
Proper separation of the two holes' apparent horizons during inspiral
The separation of the holes decreases by about a factor of two throughout the simulation.
Individual and common horizons
The individual and common apparent horizons are shown just after the common horizon forms. The wireframe mesh is colored by the value of the lapse.
Simulations
Four Areas of Science
Inspiration
Now, here, you see, it takes all the running you can do, to keep in the same place. If you want to get somewhere else, you must run twice as fast as that.