With our latest preprint [arXiv:2306.03148] (led by Cornell graduate student Jooheon Yoo), we present a numerical relativity surrogate model trained on SXS waveforms with memory effects and post-Newtonian hybridization! So what’s the hype about?!
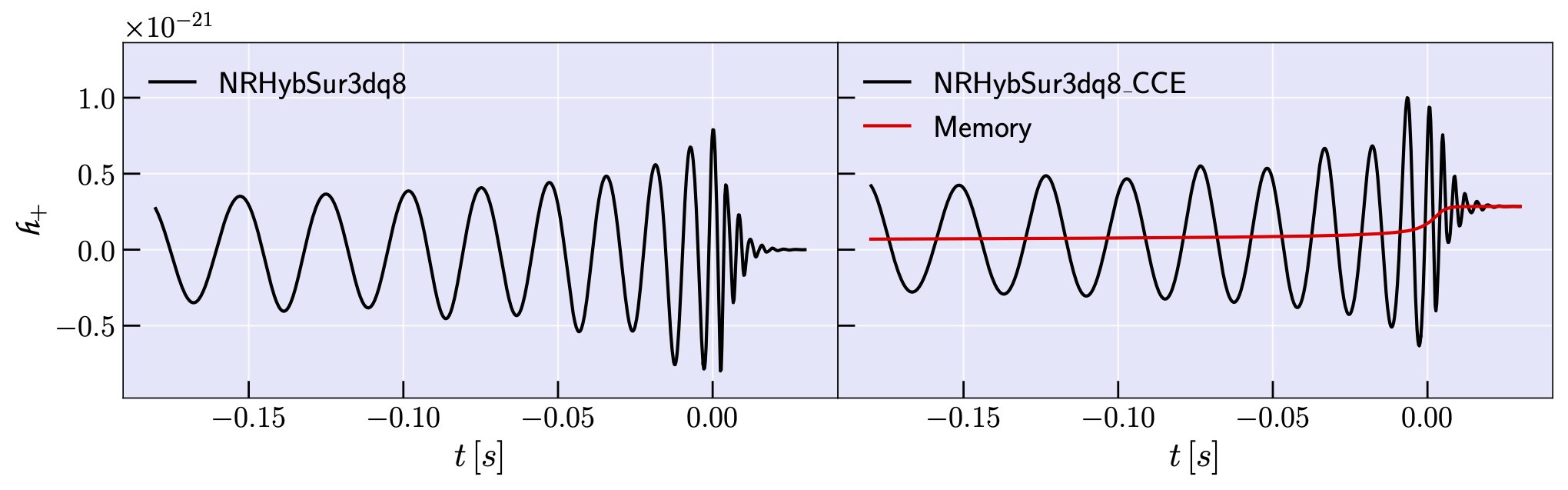
In this work we present a state-of-the-art gravitational wave surrogate model, NRHybSur3dq8_CCE, which is the first of its kind to feature everyone’s favorite phenomena: memory effects!
But what exactly is a surrogate model and how did we build ours?
When we detect a gravitational wave (GW) on Earth from, say, a binary black hole (BBH) merger, we need a waveform model (which is a function of BBH parameters) so that we can figure out what kind of BBH emitted the GW that we observed.
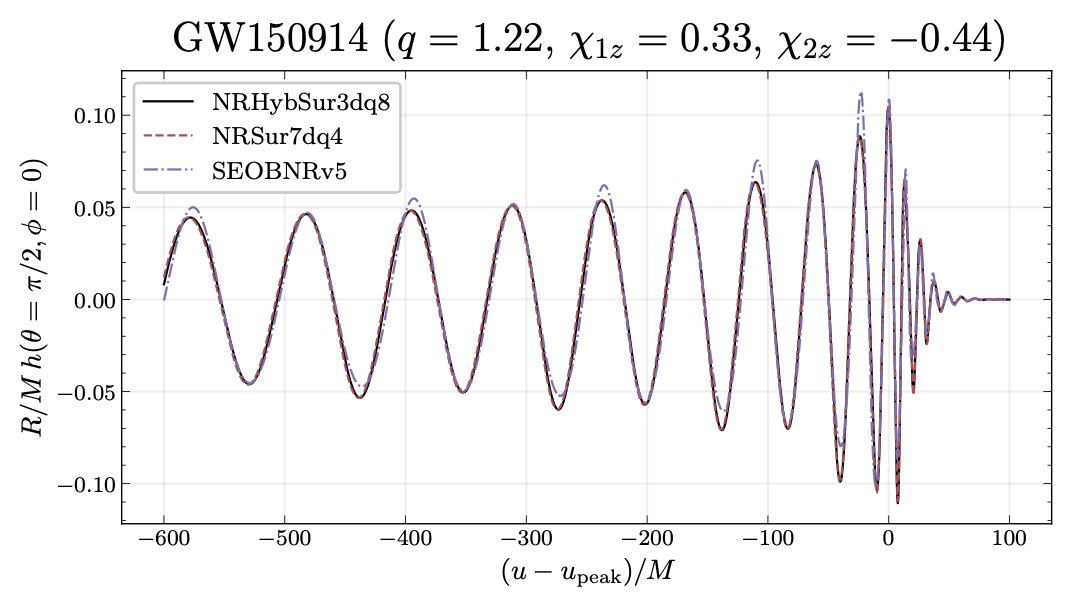
The type of waveform model which most faithfully represents numerical relativity (NR) waveforms that one can build are NR surrogate models: waveform models that are trained directly on NR waveforms rather than by making assumptions about what the waveforms should look like.
Up until now, NR surrogate models have been trained on waveforms that have been extracted to future null infinity (i.e., a place far away from the BBH that is a fairly nice approximation for what we see on Earth) using a technique called extrapolation.
But it turns out that extrapolation doesn’t capture memory effects, which are important predictions of GR! Consequently, NR surrogate models built from extrapolated waveforms won’t contain all of the gravitational wave physics that we expect to observe from BBHs.
So what are memory effects? The most common memory effect is known as the displacement memory and it corresponds to the permanent net displacement that two initially comoving observers will experience due to gravitational radiation.
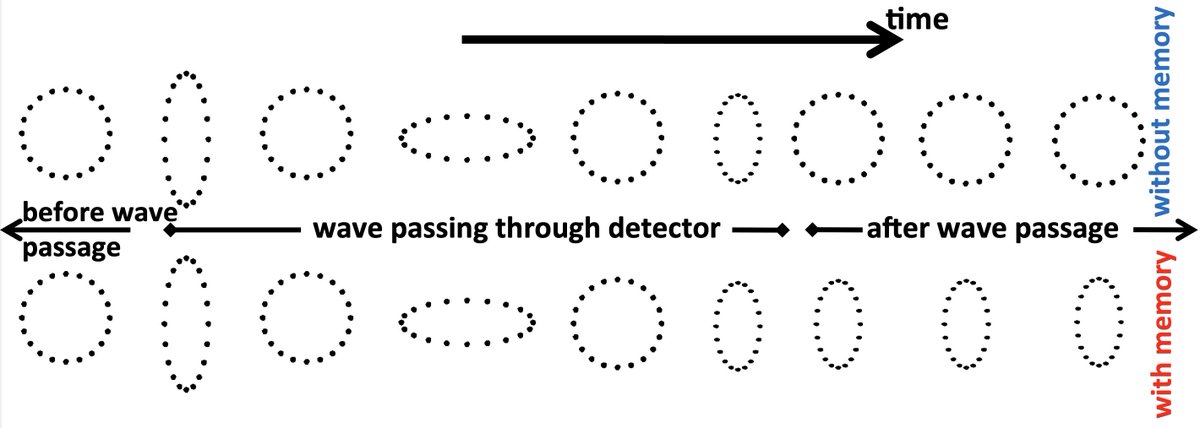
What’s so freaking cool about memory though is that it turns out that memory is intimately related to an infinite number of symmetries at future null infinity that we call BMS symmetries.
Therefore, memory is closely connected to various conservation laws of GR (thanks Emmy Noether!). And, because conservation laws help us understand quantum formulations of classical theories, perhaps memory can help us formulate a quantum theory of gravity…
Back to NR waveforms! Fortunately, there is an alternative waveform extraction technique, CCE, that does resolve memory! So let’s just build an NR surrogate model using CCE waveforms.
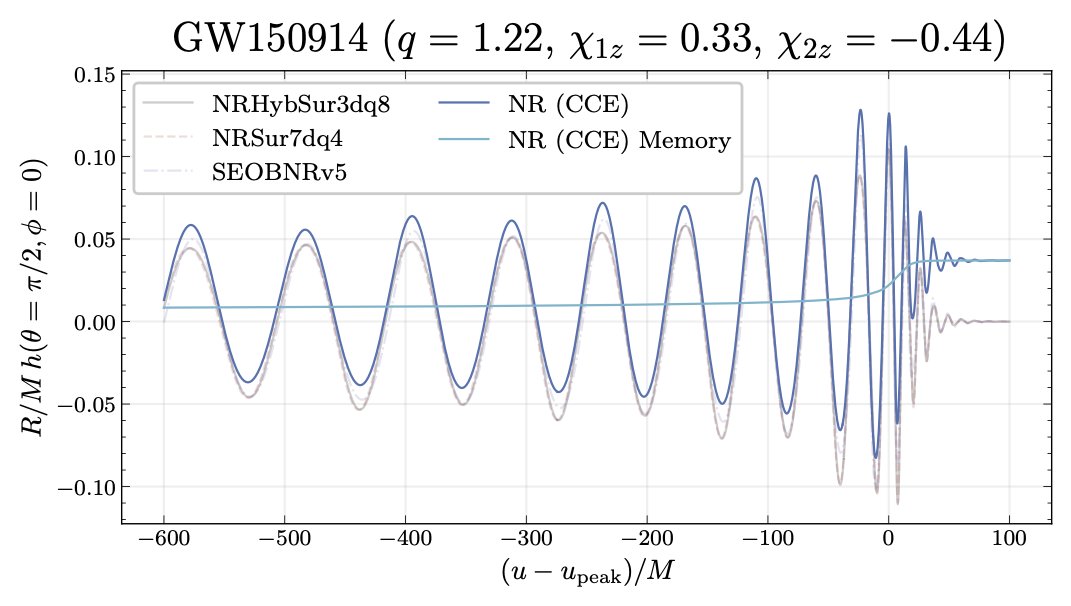
Or, even better, since NR waveforms are finite in length and therefore don’t cover the entire frequency band of our detectors, let’s instead build an NR surrogate model using hybridization (i.e., a stitching together) of CCE and post-Newtonian (PN) waveforms.
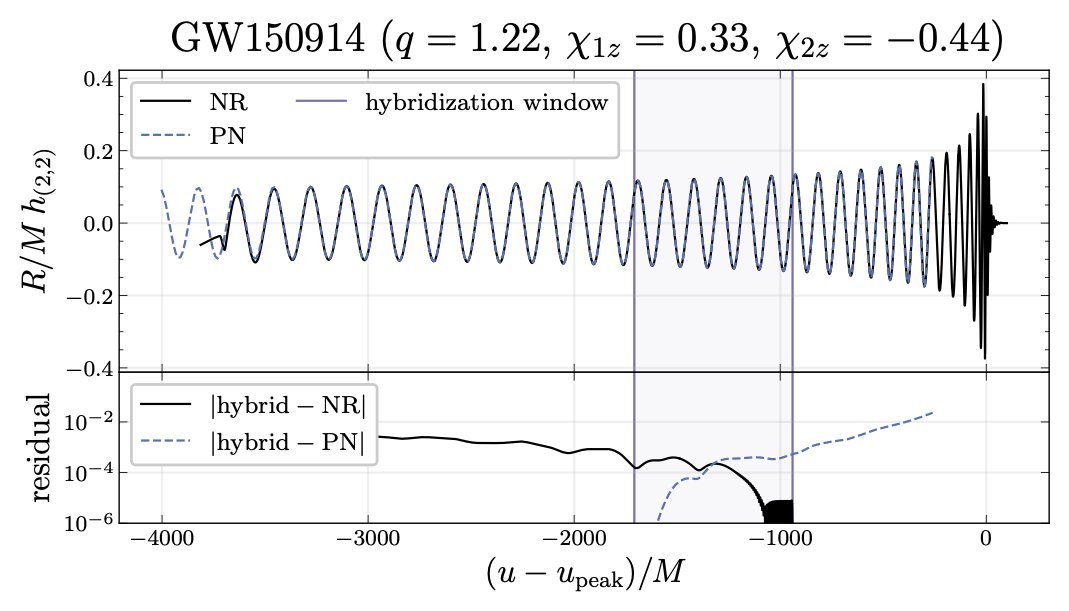
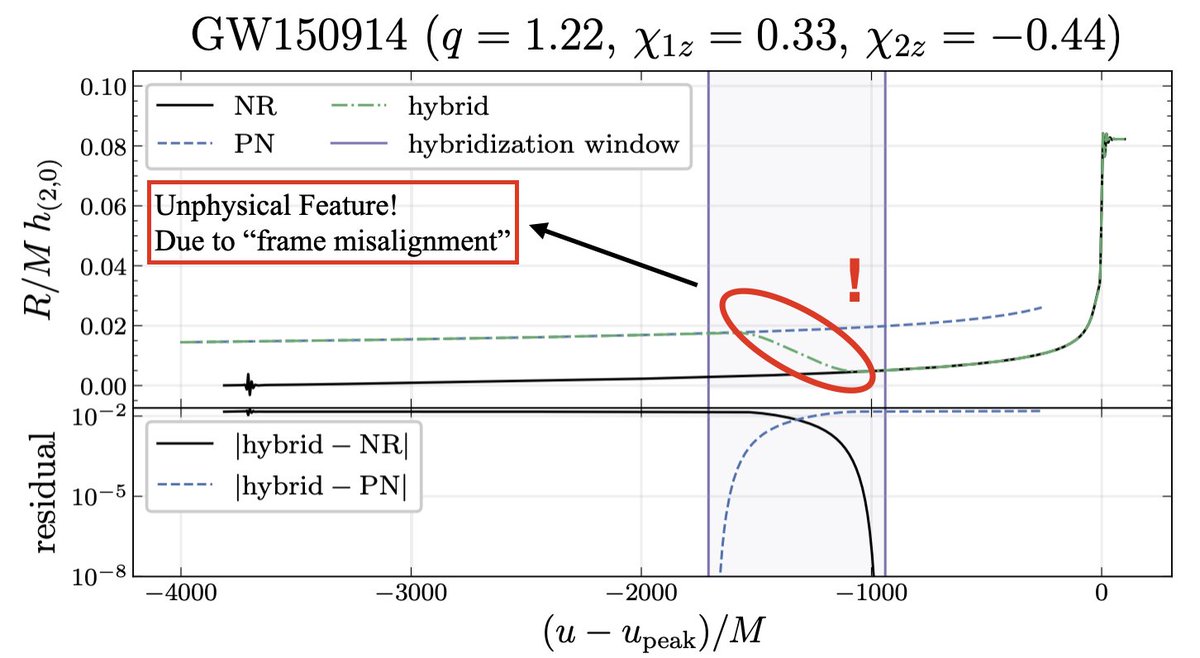
This is where the fun begins. Because when NR waveforms have memory effects, hybridizing them with PN isn’t easy! In fact, it turns out that you need to map NR waveforms to a BMS frame called the PN BMS frame or else you’ll obtain unphysical effects.
Ok, so now that we have our fancy pants hybrid waveforms, let’s build the surrogate! We build the surrogate from 102 waveforms for BBHs with mass ratios <= 8 and spins with z-components (i.e., in the direction of the orbital angular momentum) in the range [-0.8, 0.8].
There’s a lot of details involved in constructing the surrogate that we won’t try to describe here (read the paper!), but the punchline is that the new surrogate model is better than the version built with extrapolated waveforms!

Furthermore, the new surrogate accurately captures memory effects!
That’s it folks. There’s so much more in the paper so please do take a look sometime! But know that this is only the beginning. Watch our for many more surrogate models with memory effects in the near future!